Question

A man who moves to a new city sees that there are two routes he could take to work. A neighbor who has lived there a long time he tells him Route A will average 5 minutes faster than Route B.The man decides to experiment. Each day he flips a coin to determine which way to go, driving each route 10 days. He finds that Route A takes an average of 49 minutes, with standard deviation 2 minutes, and Route B takes an average of 50 minutes, with standard deviation 4 minutes. Histograms of travel times for the routes are roughly symmetric and show no outliers. (alpha =0.05)

Find a 95% confidence interval for the difference between the Route B and Route A commuting times.

Answer 1

The 95% confidence interval for the difference between the Route B and Route A commuting times is -3.771808 to 1.771808

Explanation:

Here we have the confidence interval is given by the following equation;

`\left (\bar{x}_1-\bar{x}_(2) \right ) - z_(c)\sqrt{(\sigma _(1)^(2))/(n_(1))-(\sigma _(2)^(2))/(n_(2))}< \mu _(1)-\mu _(2)< \left (\bar{x}_1-\bar{x}_(2) \right ) + z_(c)\sqrt{(\sigma _(1)^(2))/(n_(1))-(\sigma _(2)^(2))/(n_(2))}`

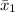`\bar x_1` = 49 Minutes

σ₁ = 2 Minutes

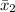`\bar x_2` = 50 Minutes

σ₂ = 4 Minutes

n₁ = n₂ = 10 days

α = 0.05

At 95%, from the z score table , z
`_c` =
`\pm`1.959964 ≈ ± 1.96

Plugging in the values Solving we get

Δμ Min = -3.771808 and Δμ Max = 1.771808.