Question

A food company sells salmon to various customers. The mean weight of the salmon is 37 lb with a standard deviation of 2 lbs. The company ships them to restaurants in boxes of 9 ​salmon, to grocery stores in cartons of 49 ​salmon, and to discount outlet stores in pallets of 64 salmon. To forecast​ costs, the shipping department needs to estimate the standard deviation of the mean weight of the salmon in each type of shipment.

Answer 1

The standard deviation for the mean weigth of Salmon is 2/3 lbs for restaurants, 2/7 lbs for grocery stores and 1/4 lbs for discount order stores.

Explanation:

The mean sample of the sum of n random variables is

`\overline{X} = (X_1+X_2+...+X_n)/(n)`

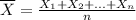
If
`X_1, ..., X_n` are indentically distributed and independent, like in the situation of the problem, then the variance of
`X_1 + .... + X_n` will be the sum of the variances, in other words, it will be n times the variance of
`X_1` .

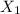However if we multiply this mean by 1/n (in other words, divide by n), then we have to divide the variance by 1/n², thus
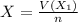`\overkine{X} = (V(X_1))/(n)` and as a result, the standard deviation of
`\overline{X}` is the standard deviation of
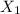`X_1` divided by
`√(n)` .

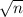Since the standard deviation of the weigth of a Salmon is 2 lbs, then the standard deviations for the mean weigth will be:

• Restaurants: We have boxes with 9 salmon each, so it will be
  `(2)/(√(9)) = (2)/(3)`
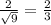
• Grocery stores: Each carton has 49 salmon, thus the standard deviation is
  `(2)/(√(49)) = (2)/(7)`
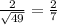
• Discount outlet stores: Each pallet has 64 salmon, as a result, the standard deviation is
  `(2)/(√(64)) = (1)/(4)`

We conclude that de standard deivation of the mean weigth of salmon of the types of shipment given is: 2/3 lbs for restaurants, 2/7 lbs for grocery stores and 1/4 lbs for discount outlet stores.