Answer:
Standard error of the proportion = 0.04702
Explanation:
Explanation:-
According to a survey by the Better Sleep Council, 33% of people admit to dozing off at their workplace
The sample proportion p = 33% = 0.33
q = 1-p = 1-0.33 = 0.67
Given a random sample of 100 workers is selected from this population
Given sample size 'n' = 100
The standard error of the Proportion is determined by
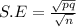
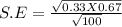
Final answer:-
Standard error of the proportion = 0.04702