Question

A government bureau publishes annual price figures for new mobile homes. A simple random sample of 36 new mobile homes yielded the following​ prices, in thousands of dollars. Assume that the population standard deviation of all such prices is ​$7.5 ​thousand, that​ is, ​$7 comma 500. Use the data to obtain a​ 99.7% confidence interval for the mean price of all new mobile homes.

Answer 1

The 99.7% confidence interval for the mean price of all new mobile homes is ($60,672, $65,622).

Explanation:

The question is incomplete:

The prices in thousands of dollar are:

66.6, 69.8, 58.4, 57.3, 63.1, 61.8, 56, 72.7, 61.8,

66.9, 72.6, 63.1, 58.7, 65.9, 61.1, 56.1, 49.9, 72.6,

49, 56.4, 72.6, 60.1, 65, 64.8, 56.5, 52, 53.2,

56.4, 75.4, 76.3, 60.5, 74.6, 57, 69.2, 62.7, 77.2.

We have a sample of n=36 new mobile homes.

The mean of this sample is:

`M=(1/36)\sum_(i=1)^(36)x_i=(2273.3)/(36)=63.147`

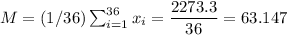
The population standard deviation is σ=7.5 (in thousands of dollars).

The critical value of z for a 99.7% CI is z=2.97.

Then, we can calculate the margin of error as:

`E=z\cdot \sigma/√(n)=2.97*7.5/√(36)=22.275/9=2.475`

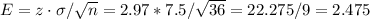
Now we can calculate the lower and upper bound of the confidence interval as:

`LL=\bar X-E=63.147-2.475=60.672\\\\UL=\bar X+E=63.147+2.475=65.622`

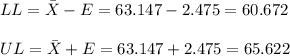
The 99.7% confidence interval for the mean price of all new mobile homes is ($60,672, $65,622).