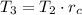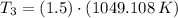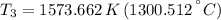Question

A cold air-standard Diesel cycle has a compression ratio of 18 and a cutoff ratio of 1.5. Determine the maximum temperature of the air and the rate of heat addition to this cycle when it produces 150 kW of power and the state of the air at the beginning of the compression is 90 kPa and 57 °C. Use constant specific heats at room temperature.

Answer 1

`\dot Q_(in) = 228.659\,kW`,
`T_(3) = 1573.662\,K\,(1300.512\,^(\textdegree)C)`

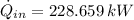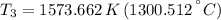
Step-by-step explanation:

The ideal efficiency of the Diesel cycle is given by this expression:

`\eta_(th) = \left\{1 - (1)/(r^(k-1)) \cdot \left[(r_(c)^(k)-1)/(k\cdot (r_(c)-1)) \right]\right\}* 100\%`

Where
`r` and
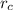`r_(c)` are the compression and cutoff ratios, respectively.

`\eta_(th) = \left\{1-(1)/(18^(0.4))\cdot \left[(1.5^(1.4)-1)/(1.4\cdot (1.5-1)) \right] \right\}* 100\%`

`\eta_(th) = 65.648\,\%`

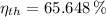
The heat addition to the cycle is:

`\dot Q_(in) = (\dot W)/(\eta_(th))`

`\dot Q_(in) = (150\,kW)/(0.656)`

`\dot Q_(in) = 228.659\,kW`

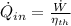
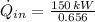
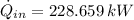
The temperature at state 2 is:

`T_(2) = T_(1) \cdot r^(k-1)`

`T_(2) = (330.15\,K)\cdot 18^(0.4)`

`T_(2) = 1049.108\,K\,(775.958\,^(\textdegree)C)`

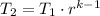
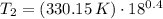
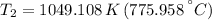
And the temperature at state 3 is:

`T_(3) = T_(2)\cdot r_(c)`

`T_(3) = (1.5)\cdot (1049.108\,K)`

`T_(3) = 1573.662\,K\,(1300.512\,^(\textdegree)C)`