Question

Congress regulates corporate fuel economy and sets an annual gas mileage for cars. A company with a large fleet of cars hopes to meet the goal of 38.2 mpg or better for their fleet of cars. To see if the goal is being​ met, they check the gasoline usage for 36 company trips chosen at​ random, finding a mean of 40.20 mpg and a standard deviation of 3.04 mpg.

Is this strong evidence that they have attained their fuel economy​ goal? Use 0.05 as the​ P-value cutoff level.

Answer 1

The calculated value t= 3,947 > 2.0301 at 0.05 level of significance ( two tailed test) with 35 degrees of freedom.

Null hypothesis is rejected

There is no strong evidence that they have attained their fuel economy​ goal.

Explanation:

Step (i):-

A company with a large fleet of cars hopes to meet the goal of 38.2 mpg or better for their fleet of cars.

Population mean 'μ' = 38.2mpg

Given the gasoline usage for 36 company trips chosen at​ random, finding a mean of 40.20 mpg and a standard deviation of 3.04 mpg.

Sample size 'n' = 36

mean of the Sample 'x⁻' = 40.20mpg

standard deviation of the Sample 'S' = 3.04 mpg.

Step(ii):-

Null hypothesis: H₀: 'μ' = 38.2mpg

Alternative hypothesis: H₁: 'μ' ≠ 38.2mpg

Level of significance ∝=0.05

The test of hypothesis

`t = (x^(-) - mean)/((S)/(√(n) ) )`

`t = (40.20- 38.20)/((3.04)/(√(36) ) ) = 3.947`

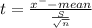
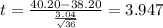
The degrees of freedom ν= n-1 = 36-1 =35

The tabulated value t₀.₀₅ = 2.0301 at 0.05 level of significance ( two tailed test) with 35 degrees of freedom.

The calculated value t= 3,947 > 2.0301 at 0.05 level of significance ( two tailed test) with 35 degrees of freedom.

Null hypothesis is rejected

Conclusion:-

There is no strong evidence that they have attained their fuel economy​ goal.