Question

The lifespans of lions in a particular zoo are normally distributed. The average lion lives 12.5 years and the standard deviation is 2.4 years.

What is the probability a lion living less than 10.1 years?

Answer 1

16%

Explanation:

Answer was correct on Khan Academy

Answer 2

`P(X<10.1)=P((X-\mu)/(\sigma)<(10.1-\mu)/(\sigma))=P(Z<(10.1-12.5)/(2.4))=P(z<-1)`

And we can find this probability with the normal standard distirbution or excel:

`P(z<-1)=0.1587`

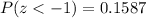
And then the probability that a lion lives less than 10.1 years is 0.1587

Explanation:

Let X the random variable that represent the lifespans of lions population, and for this case we know the distribution for X is given by:

`X \sim N(12.5,2.4)`

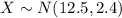
Where
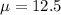`\mu=12.5` and
`\sigma=2.4`

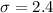
We want to find this probability:

`P(X<10.1)`

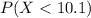
And we can use the z score formula givrn by:

`z=(x-\mu)/(\sigma)`

If we apply this formula to our probability we got this:

`P(X<10.1)=P((X-\mu)/(\sigma)<(10.1-\mu)/(\sigma))=P(Z<(10.1-12.5)/(2.4))=P(z<-1)`

And we can find this probability with the normal standard distirbution or excel:

`P(z<-1)=0.1587`

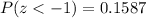
And then the probability that a lion lives less than 10.1 years is 0.1587