Answer:
![v=\sqrt[]{(2K)/(m) }](https://img.qammunity.org/2021/formulas/mathematics/middle-school/d15d9luokrs3hisi6i5y8irzwgnbei86ud.png)
Explanation:
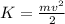
First, multiply by 2 to get rid of the 2 in the denominator. Remember that if you make any changes you have to make sure the equation keeps balanced, so do it on both sides as following;
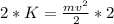
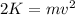
Divide by m to isolate
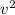 .
.
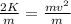
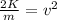
To eliminate the square and isolate v, extract the square root.
![\sqrt[]{(2K)/(m) }=\sqrt[]{v^2}](https://img.qammunity.org/2021/formulas/mathematics/middle-school/qaa3b0wahoyezwcazu1bdyd37zlgts5nra.png)
![\sqrt[]{(2K)/(m) }=v](https://img.qammunity.org/2021/formulas/mathematics/middle-school/zuibrmkqaz36ex5mqstzpqzticjbxziz78.png)
let's rewrite it in a way that v is in the left side.
![v=\sqrt[]{(2K)/(m) }](https://img.qammunity.org/2021/formulas/mathematics/middle-school/d15d9luokrs3hisi6i5y8irzwgnbei86ud.png)