Question

The doubling time of a bacterial population is 15 minutes. After 80 minutes, the bacterial population was 60000.

-What was the initial population of bacteria?

-Using your rounded answer from above, find the size of the bacterial population after 3 hours.

Answer 1

The initial population of bacteria was 1488.

The size of the bacterial population after 3 hours will be 6,084,093

Explanation:

The population of bacteria after t minutes can be modeled by the following equation.

`P(t) = P(0)e^(rt)`

In which P(0) is the initial population and r is the growth rate.

The doubling time of a bacterial population is 15 minutes.

This means that
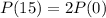`P(15) = 2P(0)`. We use this to find r.

`P(t) = P(0)e^(rt)`

`2P(0) = P(0)e^(15r)`

`e^(15r) = 2`

`\ln{e^(15r)} = ln(2)`

`15r = ln(2)`

`r = (ln(2))/(15)`

`r = 0.0462`

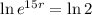
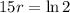
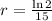
After 80 minutes, the bacterial population was 60000.

This means that
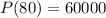`P(80) = 60000`. So

`P(t) = P(0)e^(0.0462t)`

`60000 = P(0)e^(0.0462*80)`

`P(0) = (60000)/(e^(0.0462*80))`

`P(0) = 1488`

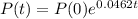
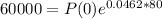
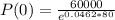
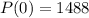
This means that the initial population of bacteria was 1488.

Using your rounded answer from above, find the size of the bacterial population after 3 hours.

t is in minutes, so this is P(3*60) = P(180).

`P(t) = 1488e^(0.0462t)`

`P(180) = 1488e^(0.0462*180)`

`P(180) = 1488e^(0.0462*180)`

`P(180) = 6,084,093`

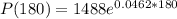
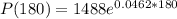
The size of the bacterial population after 3 hours will be 6,084,093