Question

Lim x^2 - 2x - 15/x^2-9

Answer 1

5/3 if x → 0, 1 if x → ∞

Explanation:

I'm going to answer this for two potential scenarios: the limit as x approaches 0, and the limit as x approaches infinity. First, let's factor and simplify our expression a little.
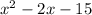`x^2-2x-15` factors into
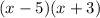`(x-5)(x+3)`, and
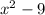`x^2-9` is the difference of squares
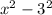`x^2-3^2`, so we can factor it into
`(x+3)(x-3)`. Our expression now becomes

`((x-5)(x+3))/((x-3)(x+3))=(x-5)/(x-3)`

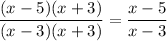
If we take the limit of this as x → 0:

`\lim_(x\to0)(x-5)/(x-3)= (-5)/(-3)=(5)/(3)`

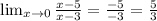
And the limit as x → ∞:

`\lim_(x\to\infty)(x-5)/(x-3) =1`

An explanation for that second limit: As x gets larger and larger, the 5 and 3 being subtracted in the numerator and denominator become less and less significant, and the fraction gets closer and closer to the value x/x, which is 1.