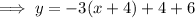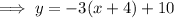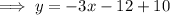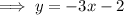Answer:
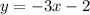
Explanation:
Slope-intercept form of a linear equation:
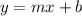
where:
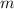 is the slope
is the slope
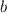 is the y-intercept
is the y-intercept
Given:
- slope (m) = -3
- y-intercept (b) = 4
Equation of line:
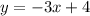
If the line is translated -4 units along the axis, we need to substitute
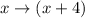
If the line is translated 6 units along the y-axis, we need to add 6 to the equation: