Question

The radius of a semicircle is 2 millimeters. What is the semicircle's perimeter?

Use 3.14 for ​.

Answer 1

do you have a picture that you can add to this

Answer 2

The perimeter of the semicircle is
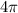`\(4\pi\)` millimeters.

The perimeter of a semicircle consists of two parts: the curved portion (half the circumference of a full circle) and the diameter (straight line across the semicircle). The formula for the perimeter (P) is given by
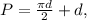`\(P = (\pi d)/(2) + d\),` where (d) is the diameter.

In this case, the radius (r) is provided, and the diameter (d) is twice the radius (d = 2r). Substituting this into the formula, we get
`\(P = (\pi * 2r)/(2) + 2r\), which simplifies to \(P = \pi r + 2r\).`

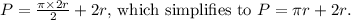
Given that the radius (r) is 2 millimeters, we substitute this value into the formula:
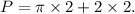`\(P = \pi * 2 + 2 * 2\).` Simplifying further, we get
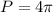`\(P = 4\pi\)` millimeters. Therefore, the perimeter of the semicircle is
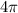`\(4\pi\)` millimeters.

Understanding the formulas for the perimeter of geometric shapes is crucial in geometry. It allows us to calculate the total distance around a figure, combining both curved and straight segments. In this case, the application of the formula to a semicircle involves using the known radius to find the perimeter.