Question

Given: AD = BC and AD || BC

Prove: ABCD is a parallelogram.
Angles
Segments Trahgles Statements Reasons
ДВСА
ADAC
Statements
Reasons
Assemble the proof by dragging tiles to
the Statements and Reasons columns.

Answer 1

hope this is what’s you need. EGDE 2020

1. AD = BC || given

Answer 2

ABCD is a parallelogram.

Explanation:

A parallelogram is a quadrilateral that has two parallel and equal pairs of opposite sides.

From the given diagram,

Given: AD = BC and AD || BC, then:

i. AB = DC (both pairs of opposite sides of a parallelogram are congruent)

ii. <ADC = < BCD and < DAB = < CBA

thus, AD || BC and AB || DC (both pairs of opposite sides of a parallelogram are parallel)

iii. < BAC = < DCA (alternate angle property)

iv. Join BD, line AC and BC are the diagonals of the quadrilateral which bisect each other. The two diagonals are at a right angle to each other.

v. <ADC + < BCD + < DAB + < CBA =
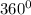`360^(0)` (sum of angles in a quadrilateral equals 4 right angles)

Therefore, ABCD is a parallelogram.