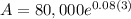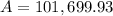Question

Suppose that $80000 is invested at 8% interest. Find the amount of money in the account after 3 years if the

interest is compounded annually. Find the amount of money in the account after 3 years if the interest is
compounded continuously.

Answer 1

Compounded Annually: $100,776.96

Compounded Continuously: $101,699.93

Explanation:

First, you are going to want to use the normal compound interest formula, which is shown below.

`A=P(1+(r)/(n) )^(nt)`

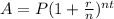
P = initial balance

r = interest rate (decimal)

n = number of times compounded annually

t = time

Change 8% into a decimal:

8% ->
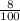`(8)/(100)` -> 0.08

Now, plug in the values into the equation:

`A=80,000(1+(0.08)/(1))^(1(3))`

`A=100,776.96`

--------------------------

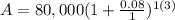
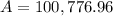
To find the interest compound continuously, use the following formula:

`A = Pe^(rt)`

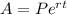
Now, plug in the values:

`A=80,000e^(0.08(3))`

`A=101,699.93`