Answer:
a) 0.2033
b) 0.5899
c) 0.2033
d) 0.9524
e) 0
f) The value that corresponds to the thinnest 10% is 5.464 lbs
g) The value that corresponds to the heaviest 8% is 8.692 lbs
h) No.
Explanation:
Hello!
Full text in last attachment.
For items a), b) and c) the variable of interests is X: Weight of a newborn baby and X~N(μ;δ²)
To calculate each of the asked probabilities, you have to first, "transform" the value of the variable to a value of the standard normal distribution Z, then you use the standard normal tables to reach the corresponding probability.
These tables show values of cumulated probabilities P(Z<
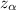)= 1 - α
a)
Symbolically:
P(X<6)
Now calculate the value of Z:
Z =(X-μ)/δ= (6-7)/1.2= -0.83
Remember, the standard normal distribution is centered in zero, so all values on the "left" of the distribution are negative and all the values on the "right" of the distribution are positive.
In the table the value of Z is divided into two, the integer and first decimal are found in the first column of the table and the second decimal value is found in the first row of the table, where these cross you'll find the corresponding probability.
The calculated value is negative so you have to use the "left" entry of the Z-table. Check attachment.
P(Z<-0.83)= 0.2033
b)
Symbolically:
P(5.8≤X≤7.8)
To calculate the probability contained in the interval, you have to subtract to the probability accumulated up to the upper bond P(X≤7.8), the cumulated probability up to P(X≤5.8)
P(X≤7.8) - P(X≤5.8)
Now you standardize both values:
Z₁= (7.8-7)/1.2= 0.67 ⇒ (see attachment)
Z₂= (5.8-7)/1.2= -1 ⇒ (see attachment)
P(Z≤0.67) - P(Z≤-1.00)= 0.7486 - 0.1587= 0.5899
c)
Symbolically:
P(X>8.2)
The Z table show you probabilities accumulated up to a value of the variable, to know what is the probability above that same value, you have to do the following calculation:
Since the total value of probability under the distribution is 1, you'll subtract from it, the probability accumulated up to 8.2 lbs, symbolically
1 - P(X≤8.2)
Now you calculate the corresponding Z value:
Z= (8.2-7)/1.2= 1
And you look for the corresponding probability value:
1 - P(Z≤1.00)= 1 - 0.8413= 0.1587
For the next two items, there was a sample of n= 4 babies taken and you'll have to calculate the probabilities of obtaining certain average weights, so you have to use the distribution of the sample mean X[bar]~N(μ;δ²/n)
The mean is μ= 7
Standard deviation δ/√n= 1.2/√4= 0.6
The steps for the standardization are the same, to reach the corresponding Z value you have to do the following calculation:
Z= (X[bar]-μ)/(δ/√n)~N(0;1)
d)
Symbolically:
P(6≤X[bar]≤9)
P(X[bar]≤9) - P(X[bar]≤6)
Calculate the Z values:
Z₁= (X[bar]-μ)/(δ/√n)= (9-7)/(1.2/√4)= 3.33
Z₂= (X[bar]-μ)/(δ/√n)= (6-7)/(1.2/√4)= -1.67
P(Z≤3.33) - P(Z≤-1.67)= 1 - 0.0474= 0.9524
e)
P(X[bar]>9)= 1 - P(X[bar]≤9)= 1 - P(Z≤3.33)= 1 - 1=0
Z= (X[bar]-μ)/(δ/√n)= (9-7)/(1.2/√4)= 3.33
P(Z≤3.33)= 1
f)
The thinnest 10% corresponds to the bottom 10% weights of newborn babies.
In this example, you know the probability, and need to find out the corresponding value of the variable, symbolically:
P(X≤x₀)= 0.10
You can consider the same under the standard normal distribution:
P(Z≤z₀)= 0.10
The "bottom 10%" lies in the left tail of the distribution, which means that the value of z that accumulates 0.10 of probability is negative. To reach this value you have to look in the body of the table for the value of probability and then reach the margins for the corresponding Z value:
z₀= -1.28
And now you have to reverse the standardization:
z₀= (x₀-μ)/δ
z₀*δ= x₀-μ
x₀=(z₀*δ)+μ
x₀= (-1.28*1.2)+7= 5.464
The value that corresponds to the thinnest 10% is 5.464 lbs
g)
The heaviest 8% of the babies are found at the top of the distribution, is the "right tail" of the distribution, same as before, you have the value of probability and have to find the corresponding value of the variable X.
This value x₀ separates the top 8% of the distribution from the bottom 100-8= 92%, so you can express it as:
P(X>x₀)=0.08
-or-
P(X≤x₀)= 0.92
Considering the standard normal distribution gives you accumulated values of probability, I'll work with the second expression:
P(X≤x₀)= 0.92
P(Z≤z₀)= 0.92
z₀= 1.41
z₀= (x₀-μ)/δ
z₀*δ= x₀-μ
x₀=(z₀*δ)+μ
x₀= (1.41*1.2)+7= 8.692 lbs
The value that corresponds to the heaviest 8% is 8.692 lbs
h)
The normal distribution is centered in its mean μ, and the most common values of the variable are found around it. The further away from the mean is the observed value, the most uncommon it is.
Under this distribution, all values within one standard deviation from the mean, are the most common values, μ ± δ.
Then the more standard deviations it is from the mean, the most uncommon the value is. To know how many standard deviations 9. 2lbs is from the population mean 7 lbs you have to standardize it:
(x-μ)/δ= (9-7)/1.2= 1.67
The value is 1.67 standard deviations away from the population mean. It is not an uncommon value.
I hope this helps!