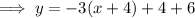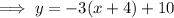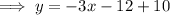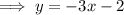Question

Suppose a line, with a slope of -3 and a y-intercept of 4, is translated -4 units along the x-axis and 6 units along the y-axis. What is the equation of this new line?

Answer 1

y = -3x - 2

Explanation:

Rules to remember :

• f(x + a) = translated 'a' units left
• f(x - a) = translated 'a' units right

Standard form of the original equation

• y = mx + b
• here m = slope and b = y-intercept
• ⇒ y = -3x + 4

Translating -4 units along the x-axis

• y = -3(x + 4) + 4
• y = -3x - 12 + 4
• y = -3x - 8

Translating 6 units along the y-axis

• y = -3x - 8 + 6
• y = -3x - 2

Answer 2

`y=-3x-2`

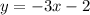
Explanation:

Slope-intercept form of a linear equation:
`y=mx+b`

where:

• 
  `m` is the slope
• 
  `b` is the y-intercept

Given:

• slope (m) = -3
• y-intercept (b) = 4

Equation of line:
`y=-3x+4`

If the line is translated -4 units along the axis, we need to substitute

`x \rightarrow (x+4)`

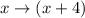
If the line is translated 6 units along the y-axis, we need to add 6 to the equation:

`\implies y=-3(x+4)+4+6`

`\implies y=-3(x+4)+10`

`\implies y=-3x-12+10`

`\implies y=-3x-2`