Question

Mars has two moons. How many objects would cause tides on Mars, if it had water

Answer 1

Both of the moon and The Sun

Explanation :

Mars is known as the fourth closest planet from the Sun. It have two satellite named Phobos and Deimos. Actually, the both of Mars's moon is just an asteroid that trapped by Mars's gravity. So, can the both of its moon make a tidal waves if Mars had water ? Yes, it can if we calculate the Newtonian Gravity Forces.

We know that :

• mp = mass of Phobos = 1.06 × 10^16 kg
• md = mass of Deimos = 1,5 × 10^15 kg
• mm = mass of Mars = 6,4 × 10^23 kg
• rp = radius of Phobos from Mars = 9376 km = 9,376 × 10^6 m
• rd = radius of Deimos from Mars = 23463 km = 23,46 × 10^6 m
• G = gravity coefisien = 6.67 × 10^-11 N.m^2.kg^-2

So, we can calculate the Phobos force to Mars

`F_p = G * { (m_m * m_p)/(r^(2))} \\ F_p = 6.67 × 10^(-11)* {(6.4 * 10^(23) * 1.5 * 10^(15))/((9.376 × 10^6)^(2))} \\ F_p = \frac{6.67 * 6.4 * 1.5 * {10}^( - 11 + 23 + 15) }{* {10}^(12) } \\ F_p = \frac{45.04 * {10}^(28) }{87.9 * {10}^(12) } \\ F_p= 0.512 * {10}^(16) = 5.12 * {10}^(15) N`

We can calculate the Deimos force to Mars

`F_d = G * { (m_m * m_d)/(r^(2))} \\ F_d = 6.67 × 10^(-11)* {(6.4 * 10^(23) * 1.06 * 10^(16))/((23.46 × 10^6)^(2))} \\ F_d = \frac{6.67 * 6.4 * 1.5 * {10}^( - 11 + 23 + 15) }{550.37 * {10}^(12) } \\ F_d = \frac{64.03* {10}^(27) }{550.37 * {10}^(12) } \\ F_d= 0.116 * {10}^(15) = 1.16 * {10}^(14) N`

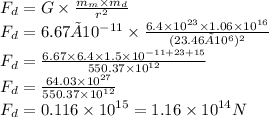
So, Phobos and Deimos still can give a huge gravity force to the Mars and can cause tidal wave.

Subject : Physics

Keyword: Gravity Forces; Tidal Waves

Answer 2

Answer: Both of the moons, the sun, and mars

Step-by-step explanation: