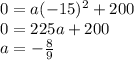Question

Please help me with math!! ​

Answer 1

Answer:
`y = -(8)/(9) (x-15)^2+200`

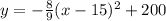
Explanation:

To answer this, we have to use quadratic equations.

We can represent this by using information given to us.

Knowing that a parabola peaks at its vertex, and the flare goes from its launch site (x = 0) and hits the ground 30m from the launch site (x = 30), we know that the flare peaks 15 meters away horizontally from the launch point.

We also know that the y-intercept is 0, because it is fired from the ground.

Knowing that the vertex for the parabola is (15, 200) and the y-intercept is (0, 0), we can model an equation.

Vertex form is:

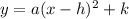`y = a(x-h)^(2) + k`, where (h, k) is the vertex.

`y = a(x-15)^2+200`

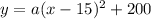
We can plug the y-intercept, (0, 0), into this equation to find a:

`0 = a(-15)^2 + 200\\0 = 225a+200\\a = -(8)/(9)`