Question

The principal at Crest Middle School, which enrolls only sixth-grade students and seventh-grade students, is interested in determining how much time students at that school spend on homework each night. The table below shows the mean and standard deviation of the amount of time spent on homework each night (in minutes) for a random sample of 20 sixth-grade students and a separate random sample of 20 seventh-grade students at this school.Based on dotplots of these data, it is not unreasonable to assume that the distribution of times for each grade were approximately normally distributed.

Estimate the difference in mean times spent on homework for all sixth- and seventh-grade students in this school using an interval. Be sure to interpret your interval.

An assistant principal reasoned that a much narrower confidence interval could be obtained if the students were paired based on their responses; for example, pairing the sixth-grade student and the seventh-grade student with the highest number of minutes spent on homework, the sixth-grade student and seventh-grade student with the next highest number of minutes spent on homework, and so on. Is the assistant principal correct in thinking that matching students in this way and then computing a matched-pairs confidence interval for the mean difference in time spent on homework is a better procedure than the one used in part (a) ? Explain why or why not.

Answer 1

a) [ -27.208 , -12.192 ]

b) New procedure is not recommended

Explanation:

Solution:-

- It is much more common for a statistical analyst to be interested in the difference between means than in the specific values of the means themselves.

- The principal at Crest Middle School collects data on how much time students at that school spend on homework each night.

- He/She takes a " random " sample of n = 20 from a sixth and seventh grades students from the school population to conduct a statistical analysis.

- The summary of sample mean ( x1 & x2 ) and sample standard deviation ( s1 & s2 ) of the amount of time spent on homework each night (in minutes) for each grade of students is given below:

Mean ( xi ) Standard deviation ( si )

Sixth grade students 27.3 10.8

Seventh grade students 47.0 12.4

- We will first check the normality of sample distributions.

• We see that sample are "randomly" selected.
• The mean times are independent for each group
• The groups are selected independent " sixth " and " seventh" grades.

• The means of both groups are conforms to 10% condition of normality.

Hence, we will assume that the samples are normally distributed.

- We are to construct a 95% confidence interval for the difference in means ( u1 and u2 ).

- Under the assumption of normality we have the following assumptions for difference in mean of independent populations:

• Population mean of 6th grade ( u1 ) ≈ sample mean of 6th grade ( x1 )

• Population mean of 7th grade ( u2 ) ≈ sample mean of 6th grade ( x2 )

Therefore, the difference in population mean has the following mean ( u ^ ):

u^ = u1 - u2 = x1 - x2

u^ = 27.3 - 47.0

u^ = -19.7

- Similarly, we will estimate the standard deviation (Standard Error) for a population ( σ^ ) represented by difference in mean. The appropriate relation for point estimation of standard deviation of difference in means is given below:

σ^ = √ [ ( σ1 ^2 / n1 ) + ( σ2 ^2 / n2 ) ]

Where,

σ1 ^2 : The population variance for sixth grade student.

σ2 ^2 : The population variance for sixth grade student.

n1 = n2 = n : The sample size taken from both populations.

Therefore,

σ^ = √ [ ( 2*σ1 ^2 / n )].

- Here we will assume equal population variances : σ1 ≈ σ2 ≈ σ is "unknown". We can reasonably assume the variation in students in general for the different grade remains somewhat constant owing to other reasons and the same pattern is observed across.

- The estimated standard deviation ( σ^ ) of difference in means is given by:

σ^ =

`s_p*\sqrt{(1)/(n_1) + (1)/(n_2) } = s_p*\sqrt{(1)/(n) + (1)/(n) } = s_p*\sqrt{(2)/(n)}\\\\\\s_p = \sqrt{((n_1 - 1 )*s_1^2 + (n_2 - 1 )*s_2^2)/(n_1+n_2-2) } = \sqrt{((n - 1 )*s_1^2 + (n - 1 )*s_2^2)/(n+n-2) } = \sqrt{((n - 1 )*s_1^2 + (n - 1 )*s_2^2)/(2n-2) } \\\\s_p = \sqrt{((20 - 1 )*s_1^2 + (20 - 1 )*s_2^2)/(2(20)-2) } \\\\s_p = \sqrt{(19*10.8^2 + 19*12.4^2)/(38) } = √(135.2) \\\\s_p = 11.62755`

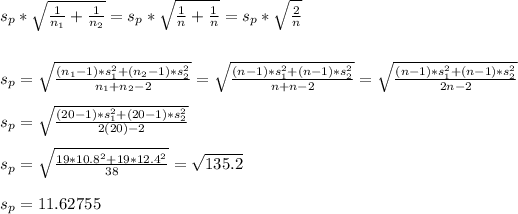
σ^ = 11.62755*√2/20

σ^ = 3.67695

- Now we will determine the critical value associated with Confidence interval ( CI ) which is defined by the standard probability of significance level ( α ). Such that:

Significance Level ( α ) = 1 - CI = 1 - 0.95 = 0.05

- The reasonable distribution ( T or Z ) would be determined on the basis of following conditions:

• The population variances ( σ1 ≈ σ2 ≈ σ ) are unknown.
• The sample sizes ( n1 & n2 ) are < 30.

Hence, the above two conditions specify the use of T distribution critical value. The degree of freedom ( v ) for the given statistics is given by:

v = n1 + n2 - 2 = 2n - 2 = 2*20 - 2

v = 38 degrees of freedom

- The t-critical value is defined by the half of significance level ( α / 2 ) and degree of freedom ( v ) as follows:

t-critical = t_α / 2, v = t_0.025,38 = 2.024

- Then construct the interval for 95% confidence as follows:

[ u^ - t-critical*σ^ , u^ + t-critical*σ^ ]

[ -19.7 - 2.042*3.67695 , -19.7 + 2.042*3.67695 ]

[ -19.7 - 7.5083319 , -19.7 + 7.5083319 ]

[ -27.208 , -12.192 ]

- The principal should be 95% confident that the difference in mean times spent of homework for ALL 6th and 7th grade students in this school (population) lies between: [ -27.208 , -12.192 ]

- The procedure that the matched-pairs confidence interval for the mean difference in time spent on homework prescribes the integration of time across different sample groups.

- If we integrate the times of students of different grades we would have to make further assumptions like:

• The intelligence levels of different grade students are same
• The aptitude of students from different grades are the same
• The efficiency of different grades are the same.

- We have to see that both samples are inherently different and must be treated as separate independent groups. Therefore, the above added assumptions are not justified to be used for the given statistics. The procedure would be more bias; hence, not recommended.