Answer:
a) Maximum altitude of the projectile,
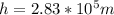
b) v = 10885.7 m/s
Step-by-step explanation:
a) Mass of the earth,
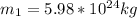
Mass of the projectile =

Launch speed, v = 2.31 * 10³ m/s
Earth radius, r = 6.36 ✕ 10⁶ m
Workdone by the projectile against gravity

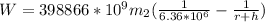 ...............(1)
...............(1)
Kinetic energy of the projectile:
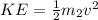
 ...................(2)
...................(2)
Equating (1) and (2) based on the law of energy conservation
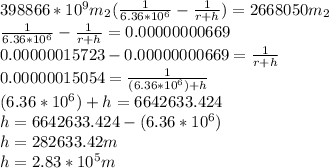
b) Smallest required change in the satellite speed
Altitude, h = 352 km = 352000 m
Earth radius, r = 6.38 * 10⁶ m
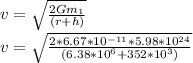
v = 10885.7 m/s