Question:
a. A = (2πr)(r)
b. A = (2πr)(2r)
c.
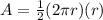
d.

Answer:
The correct option is
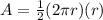
Explanation:
The formula for the area, A of a parallelogram = base, b × height, h
Therefore, since the base dimension is approximately half the perimeter of a circle, we have;
Base, b = 2·π·r × 1/2
Where the height of the parallelogram, as shown in the diagram is approximately the radius of the circle, we have;
Height, h = r
Therefore, the approximate area, A of the parallelogram is given by the following relation;
A = b × h = 2·π·r × 1/2 × r Which is the same as A =
 .
.