Answer:
Approximately
 .
.
Step-by-step explanation:
In the earth's atmosphere, the speed of radio waves is very close to that of light in vacuum.
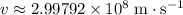 .
.- In other words, the radio wave from the station would travel
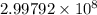 meters in each second.
meters in each second. - Note that the answer should have three significant figures. To avoid rounding errors, make sure all intermediate values have more significant figures than that. Here,
 has six significant figures.
has six significant figures.
The frequency
 of a wave gives the number of cycles in unit time. That's the same as the number of wavelengths that this wave covers in unit time.
of a wave gives the number of cycles in unit time. That's the same as the number of wavelengths that this wave covers in unit time.
In this question,
 . In other words, in each second, this wave would travel a distance that's equal to
. In other words, in each second, this wave would travel a distance that's equal to
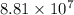 times its wavelength.
times its wavelength.
Let
 represent the wavelength of this wave.
represent the wavelength of this wave.
 .
.
Hence the equation:
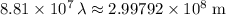 .
.
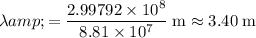 .
.
(Rounded to three significant figures.)
In general, if a wave has speed
 and frequency
and frequency
 , then its wavelength would be:
, then its wavelength would be:
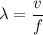 .
.