Question

Write the coordinate point −2 + 2i in polar form.

Answer 1

Answer:IDK

Step-by-step explanation:it depends on the graph

Answer 2

(2
`√(2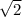)`, 135° )

Explanation:

To convert from rectangular to polar form, that is

(x, y ) → (r, Θ ), with

r =
`√(x^2+y^2)`

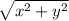
tanΘ =
`(y)/(x)`

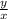
Given - 2 + 2i, then

r =
`√((-2)^2+2^2)` =
`√(4+4)` =
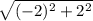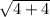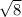`√(8)` = 2
`√(2)`

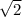
Since - 2 + 2i is in the second quadrant then Θ must be in the second quadrant.

tanΘ =
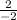`(2)/(-2)` = - 1, thus

Θ =
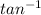`tan^(-1)` (- 1) = - 45°, hence

Θ = 180° - 45° = 135° ← in second quadrant

Thus

- 2 + 2i → (2
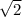`√(2)`, 135° )