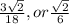Question

Can someone help me ASAP please (radical expressions)

Answer 1

Answer: B.

Explanation:

You can rationalize a denominator by multiplying both the numerator and denominator by the radical in the denominator. In this case, it is the square root of 6.

`(√(3)*√(6) )/(3√(6)*√(6) )`

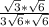
The square root of 6 multiplied by the square root of 6 is equal to 6, so you can simplify the equation to this:

`(√(3) *√(6) )/(18)`

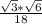
You can multiply simplified radicals together. First, check that 3 and 6 are simplified (their multiples do not include squares. If 8 was in one of the radicals, it could be simplified to 2*square root of 2.)

`√(3 ) *√(6) = √(18)`

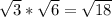
Because 18 can be simplified to 9 * 2, and 9 is a square of 3, you can simplify this to
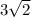`3√(2)`.

`(3√(2) )/(18) , or (√(2) )/(6)`