Question

Given: R=2m

KL = LM = KM
Find: V and
Surface Area of the cone

Answer 1

The volume of the cone is 3π≈9.42.

The surface area of the cone is 9π≈28.27.

Explanation:

If we make a section of the sphere and the cone, we have a equilateral triangle inscribed in a circle (see picture attached).

We only know the numerical value of the radius R, that is 2 m.

From the picture, we have

`\bar{KM}=2\cdot R\cdot cos(30^(\circ))=2R(√(3))/(2)=√(3)R= 2√(3)`

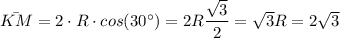
The radius of the base of the cone is

`r=\bar{KO}=\bar {KM}/2=(2√(3))/2=√(3)`

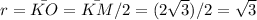
The height of the cone can be calculated as:

`h=\bar{LO}=\bar{KL}\cdot cos(30^(\circ))=(2√(3))*(√(3)/2})=3`

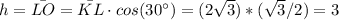
The volume of the cone can be calculated as:

`V=(1)/(3)\pi r^2h=(1)/(3)\pi (√(3))^2*3=3\pi\approx9.42`

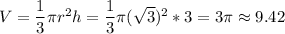
The surface area of the cone is:

`S=S_(base)+S_(face)=\pi r^2+\pi r l=\pi r^2+\pi r (\bar{KL})\\\\S=\pi(√(3))^2+\pi √(3)*2√(3)=3\pi+2\pi*3=(3+6)\pi=9\pi\approx 28.27`