Question

PLEASE HELP WITH B OR C ASAP ❤️

Answer 1

Answers and Step-by-step explanations:

(b) We see that this figure is made up of 3 congruent isosceles triangles (because two of their sides are equal to the sides of the square), 3 congruent squares, and one central equilateral triangle.

We know that all the angles of an equilateral are 60 degrees, so we can label those angles on the central triangle each as 60 degrees.

Squares all have 90 degree angles, so label all the interior angles of the squares as 90 degrees.

We also see that the angle labelled x is one of the base angles of one isosceles triangle, which means that the other base angle will also be x. This is the same for all the base angles of all 3 isosceles triangles. We know from part (a) that x = 30 degrees, so all those internal angles are 30 degrees.

Finally, in order to figure out the vertex angle of each isosceles triangle, we need to use the fact that the circled part on the attachment is 360 degrees - a circle is always 360 degrees. This 360 degree angle is made up of two angles from two squares, one angle from the equilateral triangle, and the vertex angle of the isosceles triangle. So: 360 = 90 + 90 + 60 + y (y is the vertex angle we want to find). y = 360 - 90 - 90 - 60 = 120 degrees. So, label all the vertex angles of the isosceles triangles as 120 degrees.

(c) This is a similar diagram but there are 5 isosceles triangles, 5 squares, and one central regular pentagon this time (a regular pentagon is one where all sides are equal). Use the equation:
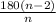`(180(n-2))/(n)` to figure out how many degrees are in each angle of a regular n-gon. Here, n = 5, so:
`(180(n-2))/(n)=(180(5-2))/(5)=(180(3))/(5)=108`. Each angle of the pentagon is 108 degrees.

Now, use the same method as before regarding the 360 degrees. We know that the circled angle on the second attachment is 360 and it's made up of one angle from the pentagon, 2 angles from 2 squares, and the vertex angle of one isosceles triangle. Then: 360 = 108 + 90 + 90 + y (y is the vertex angle we want to find). y = 72 degrees.

Finally, since this triangle is isosceles, we can find x by doing:
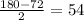`(180-72)/(2) =54` degrees. Thus, x = 54 degrees.

Hope this helps!

Answer 2

a)

Each angle of the equilateral triangle is 180/3 = 60 degrees. Each angle of the square is 90 degrees. Focus on the angles around the top vertex of the equilateral triangle. We have 2 angles from the square and one angle from the equilateral triangle, so 2*90+60 = 180+60 = 240 degrees is accounted for so far, leaving 360-240 = 120 degrees left over for the northernmost triangle.

The northernmost triangle is isosceles because the squares all have the same side lengths (due to the fact they match up with an equilateral triangle where all the sides are the same here as well). Isosceles triangles have congruent base angles, in this case both are x degrees. Add up the angles of this northernmost triangle and set this equal to 180. Solve for x.

x+120+x = 180

2x+120 = 180

2x = 180-120

2x = 60

x = 60/2

x = 30

=====================================================

b)

The angle x combines with the 90 degree adjacent angle of the square to get 90+x = 90+30 = 120. Each interior angle of this odd hexagon is 120 degrees. Focus on the entire figure overall.

====================================================

c)

The interior angles of any pentagon always add to 180(n-2) = 180(5-2) = 540 degrees. Assuming this is a regular pentagon, each interior angle of the regular pentagon is 540/5 = 108 degrees.

Focus on the northern most point on the pentagon. The angles attached to this point are the two square angles of 90 degrees each and the 108 degrees from the interior angle of a pentagon. We have 2*90+108 = 288 degrees so far, and 360-288 = 72 degrees left over for the bottom angle of the northern most triangle.

Again we have an isosceles triangle, so the base angles are both x

x+x+72 = 180

2x+72 = 180

2x = 180-72

2x = 108

x = 108/2

x = 54

And,

90+x = 90+54 = 144 represents each interior angle of this strange looking decagon.