Question

What is the value of x?

Answer 1

The value of x would be 8

Answer 2

H. x = 8

Explanation:

Let's label the vertices of the large triangle A, B, and C, and the point splitting the hypotenuse of the large triangle into the lengths x and 10 D (I've uploaded a marked up version of the problem to illustrate this step). The large triangle ABC and the small triangle ADC are similar, since they contain all three of the same angles. This means that the ratios between their corresponding sides are equal to each other. Side AB measures x + 10 and corresponds to side AC, which measures x + 4, so the ratio between their sides is
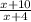`(x+10)/(x+4)`. Similarly, side AC (measuring x + 4) corresponds to the side AD (measuring x) for a ratio of
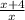`(x+4)/(x)`. Equating the two, we have

`(x+10)/(x+4)=(x+4)/(x)`

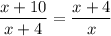
Cross multiplying, expanding and collecting like terms:

`(x+10)\cdot x=(x+4)^2\\x^2+10x=x^2+8x+16\\10x=8x+16\\2x=16\\x=8`

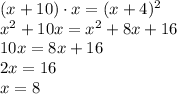
So our answer must be H. x = 8.