Answer:
The account balance will be $8,014.32
Explanation:
To calculate the future value of a certain amount invested and compounded periodically, the following formula is used:
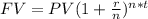
where:
FV = Future value = ???
PV = Present value = $5,838
r = interest rate in decimal = 4% = 0.04
n = number of compounding period per year = 2
t = time in years
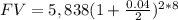
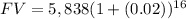
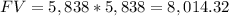
FV = $8,014.32