Answer:
w = 0.943 rad / s
Step-by-step explanation:
For this problem we can use the law of conservation of angular momentum
Starting point. With the mouse in the center
L₀ = I w₀
Where The moment of inertia (I) of a rod that rotates at one end is
I = 1/3 M L²
Final point. When the mouse is at the end of the rod
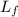 = I w + m L² w
= I w + m L² w
As the system is formed by the rod and the mouse, the forces during the movement are internal, therefore the angular momentum is conserved
L₀ = L_{f}
I w₀ = (I + m L²) w
w = I / I + m L²) w₀
We substitute the moment of inertia
w = 1/3 M L² / (1/3 M + m) L² w₀
w = 1 / 3M / (M / 3 + m) w₀
We substitute the values
w = 1/3 / (1/3 + 0.02) w₀
w = 0.943 w₀
To finish the calculation the initial angular velocity value is needed, if we assume that this value is w₀ = 1 rad / s
w = 0.943 rad / s