Question

Food and clothing are shipped to victims of a natural disaster. Each carton of food will feed 13 people, while each carton of

clothing will help 6 people. Each 20-cubic-foot box of food weighs 40 pounds and each 5-cubic-foot box of clothing weighs 20
pounds. The commercial carriers transporting food and clothing are bound by the following constraints:
- The total weight per carrier cannot exceed 23,000 pounds.
- The total volume must be no more than 9000 cubic feet.
Use this information to answer the following questions.
How many cartons of food and clothing should be sent with each plane shipment to maximize the number of people who can be
helped?

Answer 1

If we don't need to carry both types of carton, the optimal solution is 0 cartons of food and 1,800 cartons of clothes. This will help 10,800 people.

If both types of carton need to be carried, the optimal solution is 325 cartons of food and 500 cartons of clothes. This will help 7,225 people.

Explanation:

This is a linear programming problem.

We have to maximize the number of people we are helping with the shipment.

The number of people helped can be expressed as:

`P=13F+6C`

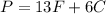
being F: cartons of food, and C: cartons of clothes.

The restrictions are Volume and Weight.

The maximum volume allowed is 9000 cubic feet.

We can express this as:

`20F+5C\leq9,000`

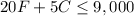
The maximum weight allowed is 23,000 pounds.

We can express this as:

`40F+20C\leq23,000`

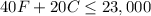
Also, we know that both quantities F and C are positive:

`F,C\geq0`

We can graph the restrictions to limit the feasible solution region (see picture attached).

There are 3 points that are defined by the saturation of 2 constraints (Note: saturation means that the restriction is expressed in this point with an equal sign).

In one of this points lies the combination of food and clothes cartons that maximizes the people helped.

The points are:

Point 1: F=0, C=1,800

`P=13F+6C=13\cdot 0+6\cdot 1,800=0+10,800\\\\P=10,800`

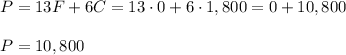
Point 2: F=575, C=0

`P=13F+6C=13\cdot 575+6\cdot 0=7,475+0\\\\P=7,475`

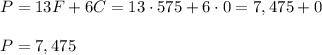
Point 3: F=325, C=500

`P=13F+6C=13\cdot 325+6\cdot 500=4,225+3,000\\\\P=7,225`

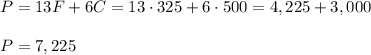
If we don't need to carry both types of carton, the optimal solution is 0 cartons of food and 1,800 cartons of clothes. This will help 10,800 people.

If both types of carton need to be carried, the optimal solution is 325 cartons of food and 500 cartons of clothes. This will help 7,225 people.