Question

PLEASE HELP!!

1) Machines that fill bags with powdered sugar, also called confectioner’s sugar, are
supposed to dispense exactly 32 ounces of powdered sugar into each bag. Let X = the weight in ounces of
the powdered sugar dispensed into a randomly selected bag. Suppose that X follows a normal distribution
with mean 32 ounces and standard deviation 0.6 ounces. Find and interpret P(X  31).

2) Refer to the previous problem. What percent of all bags contain 31 to 33 ounces of
powdered sugar?

Show work

Answer 1

Problem 1

mu = 32 is the population mean, sigma = 0.6 is the population standard deviation

Convert the raw score x = 31 into its z score

z = (x-mu)/sigma

z = (31-32)/0.6

z = -1.67 approximately

Finding
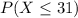`P(X \le 31)` is approximately the same as finding
`P(Z \le -1.67)`

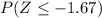
To find this value, we use a calculator or a table. I'll use a table. Specifically it is called a Z table. They are found in the back of your stats textbook. If you don't have a textbook with you, then they can be found freely online by searching out "z table".

Check out the attached image below. In that image I have marked the row that starts with -1.6 and the column that has 0.07 at the top. These two values combine to -1.67, with the value 0.0475 at the intersection of this row and column.

This means,
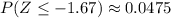`P(Z \le -1.67) \approx 0.0475` and that
`P(X \le 31) \approx 0.0475`

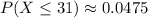
Interpretation: The probability of getting a bag of weight 31 ounces or less is approximately 0.0475 (which is a 4.75% chance roughly).

Another interpretation: Roughly 4.75% of all the bags have a weight of 31 ounces or less.

===========================================================

Problem 2

Earlier we found that x = 31 has a z score of roughly z = -1.67

Convert x = 33 to its corresponding z score and you should find that it is roughly z = 1.67

Use the Z table to find that

`P(Z \le 1.67) \approx 0.9525`

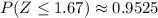
therefore,

`P(X \le 33) \approx 0.9525`

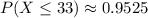
and,

`P(A \le X \le B) = P(X \le B) - P(X \le A)\\\\P(31 \le X \le 33) = P(X \le 33) - P(X \le 31)\\\\P(31 \le X \le 33) \approx 0.9525 - 0.0475\\\\P(31 \le X \le 33) \approx 0.905`

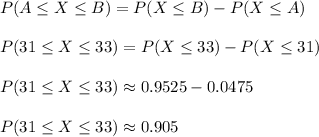
Therefore, the percent of all bags with weights between 31 and 33 ounces is roughly 90.5%