Question

Can someone please answer the bottom question. I really need help. Be sure to explain because I have no idea what I’m doing

Answer 1

See below.

Explanation:

RSTV is a quadrilateral. We see that segments RV and RS are congruent. We also see that segments TV and TS are congruent. That makes quadrilateral RSTV a kite. A kite is a quadrilateral that has one set of congruent adjacent sides and a second set of congruent adjacent sides. One set of congruent adjacent sides may or may not be congruent to the second set of congruent adjacent sides. In this case they are not.

The diagonals of a kite are perpendicular which is shown in your figure with segment VS perpendicular to segment RT. The diagonals form 4 right triangles. The 4 right triangles are VRW, SRW, VTW, and STW.

Triangles VRW and SRW are congruent.

Triangles VTW and STW are congruent.

Let's work on the angles first.

Let's work on triangle VTW.

Angle VWT is a right angle.

m<VWT = 90

m<WVT = 42

m<VWT + m<VTW + m<WVT = 180

90 + 42 + m<WVT = 180

m<WVT + 132 = 180

m<WVT = 48

Triangle SWR is a right triangle.

m<RWS + m<RSW + m<SRW = 180

90 + m<RSW + 21 = 180

m<RSW + 111 = 180

m<RSW = 69

Triangles WVR and WSR are congruent with corresponding angles WVR and WSR.

m<WVR = m<WSR = 69

m<TVR = m<WVT + m<WVR

m<TVR = 48 + 69 = 117

m<TVR = 117

Now we deal with sides.

Let's look at triangle VWT.

Side VT is the hypotenuse.

m<VTW = 42 deg

VT = 15

For angle VTW, VW is the opposite leg, and VT is the hypotenuse.

The trig ratio that relates the opposite leg and the hypotenuse is the sine.

`\sin \angle A = (opp)/(hyp)`

`\sin \angle VTW = (VW)/(VT)`

`\sin 42^\circ = (VW)/(15)`

`VW = 15 \sin 42^\circ`

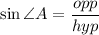
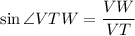
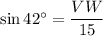
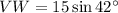
VW = 10

Since triangles RVW and RSW are congruent, corresponding sides VW and SW are congruent.

SW = VW = 10

Trianlge RSW is a right triangle with right angle RWS.

For angle WRS, SW is the opposite leg. RW is the adjacent leg.

`\tan A = (opp)/(adj)`

`\tan \angle WRS = (SW)/(RW)`

`\tan 21^\circ = (10)/(RW)`

`RW \tan 21^\circ = 10`

`RW = (10)/(\tan 21^\circ)`

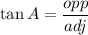
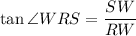
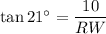
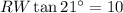
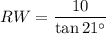
RW = 26

We now know VW and RW. Using the Pythagorean theorem we can find RV.

(RW)^2 + (VW)^2 = (RV)^2

26^2 + 10^2 = (RV)^2

RV = 28

Perimeter:

Triangles RVT and RST are congruent, so we have:

RV = RS = 28

VT = ST = 15

perimeter = RS + RV + VT + ST

perimeter = 28 + 28 + 15 + 15

perimeter = 86