Question

Given the graphs of f(x) = x – 4 and g(x) = –2x – 7, what is the solution to the equation f(x) = g(x)?

A) –7

B) –4

C) –1

D) 4

Answer 1

C) -1

Explanation:

we have the following functions:

`f(x)=x-4`

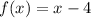
and

`g(x)=-2x-7`

to find the solution of
`f(x) = g(x)`

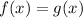
what you need to do is to match the two functions:

`f(x) = g(x)\\x-4=-2x-7`

and now we solve this equation for x.

we move the -2x to the left as a +2x, and the -4 on to the right as a +4

`x+2x=-7+4`:

and we add the quantities on both sides:

`3x=-3`

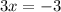
dividing by 3:

`x=-3/3\\\\x=-1`

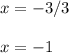
the solution to the equation is

C) -1