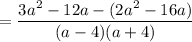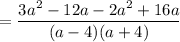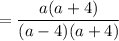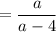Answer:
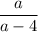
Explanation:
You are subtracting fractions, so as usual with fraction subtraction, you need a common denominator. To get a common denominator, you need to factor each denominator.
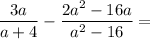
Factor the right denominator. It is a difference of two squares.
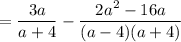
The left denominator is (a + 4). The right denominator is (a - 4)(a + 4). The LCD is (a - 4)(a + 4), so multiply the left fraction by (a - 4)/(a - 4).
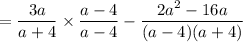
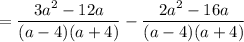
Be careful when you do the subtraction of the numerators, 3a² - 12a minus 2a² - 16a. 3a² - 12a - (2a² - 16a). The minus of the subtraction changes each sign inside the parentheses, so you end up with 3a² - 12a - 2a² + 16a. Be especially careful with the +16a.