Answer:
1
Explanation:
There's a lot to unwrap here, but thankfully we have a set of rules for unwrapping an expression like this called the order of operations. It starts with looking at any parts of the expression that are clearly grouped with parentheses. Our expression has the complex grouping
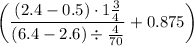
With the groupings
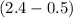 and
and
 nested inside. Let's handle those first:
nested inside. Let's handle those first:
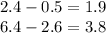
Taking these back to the larger grouped expression, we now have
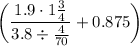
Since dividing by a fraction is the same as multiplying by its reciprocal, we can rewrite
 as
as
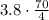 . Let's also rewrite
. Let's also rewrite
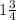 as the improper fraction
as the improper fraction
 . The fraction in the parenthesis now becomes
. The fraction in the parenthesis now becomes
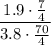
We can split this up into the expression
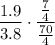
1.9 is half of 3.8, so
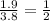 , and
, and
 , so we can finally simplify the big parentheses to read:
, so we can finally simplify the big parentheses to read:
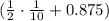
Next down from grouped expressions in the order of operations are exponents, and after that multiplication and division, which we handle from left to right. Handling the multiplication
 gives us
gives us
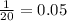 , letting us finally solve the big parentheses expression to get
, letting us finally solve the big parentheses expression to get
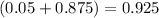 .
.
Pulling back out to the larger expression and bringing back in the last two operations, we now have the expression
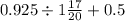 . We can rewrite
. We can rewrite
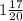 in decimal form as
in decimal form as
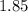 , making our expression read:
, making our expression read:
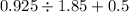
0.925 is exactly half, or 0.5, of 1.85, so we can say that
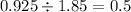 , and we're finally ready to solve our expression:
, and we're finally ready to solve our expression:
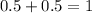
Our solution is 1. Some very hairy arithmetic for a simple answer!