Answer:
7
Explanation:
(h • g)(x) is a composite function, which essentially means that we are looking for h(g(x)), where g(x) replaces x in the function h(x).
We know that h(x) =
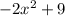 and g(x) = x/5. We want: h(g(x)) =
and g(x) = x/5. We want: h(g(x)) =
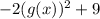 . So, just plug x/5 in for g(x):
. So, just plug x/5 in for g(x):

Now, since we want h(g(-5)), we plug -5 in for x: h(g(-5)) =
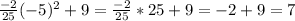
Thus, the answer is 7.
Hope this helps!