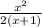Question

Simplify the complex fraction

Answer 1

Answer:
`(x^2)/(2x+2)`,

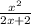Explanation:

First, simplify the denominator. Ignore the numerator for the time being.

To simplify it, we need to multiply each numerator by the opposite's denominator so we can add them together:

`(1(x+2))/(x(x+2)) + (1(x))/(x(x+2))`

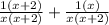
You can simplify this to get

`(2x + 2)/(x^2 + 2x)`

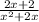
So this is your denominator when simplified. To simplify the entire fraction, we need to divide it. We can do this by reversing the numerator and denominator of the bottom fraction to
`(x^2 + 2x)/(2x+2)`. This is done when dividing fractions by fractions.

Now, it should look something like this:

`(x)/(x+2) *(x^2+2x)/(2x+2)`

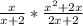
This is equal to

`(x^2(x+2))/((x+2)(2x+2))`

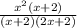
Seeing as there is a (x+2) on both the numerator and the denominator, you can eliminate it from the equation to get this:

`(x^2)/(2(x+1))`