Question

How do you solve: 7^2=12^x

Answer 1

x ≈ 1.57

Explanation:

First, note that 7^2 equals 7 * 7 = 49. Now, we have:

49 =
`12^x`

In order to solve for x, we need to use logarithm, which basically "gets rid of" the exponent. What we need to do is take the
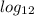`log_(12)` of each side. Notice that the base of the logarithm is 12. This is because we want to cancel out the exponent base of 12 on the right side:

`log_(12)49=log_(12)12^x`

`log_(12)49=x`

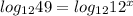
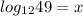
So, x ≈ 1.57.

Hope this helps!

Answer 2

x = 1.566

Explanation:

7^2=12^x

• 7^2 means 7 squared, which is 7*7, which is 49.

49 = 12^x

• Now we have to use logarithms to figure this out! Logarithms are like the opposite of exponents.

Exponential: b^x = y

Logarithmic: logb(y) = x.

• B stands for base.

• Now with 49 = y, 12 = b, we plug in to get x:

logb(y) = x

log12(49) = x

Plug this in your calculator (on a TI-84, it's MATH -> A)

x = 1.566