Answer:
Dimensions of rectangle are length = 7 cm and width = 2 cm
Explanation:
Let l = length and w = width of the rectangle.
Given that, length is 5 cm less than 6 times width. Rewriting it in equation form,
L = 6 w - 5 cm
Also given that area of rectangle is 14 cm²
Now using formula for area of rectangle,
Area of rectangle = length × width
Area of rectangle = l × w
Substituting the values,
14 = (6 w - 5) × w
Simplifying by using distributive rule,
14 = 6 w² - 5 w
To find the value of b, use the quadratic formula. So rewriting the equation in quadratic form ax²+bx+c=0
Subtracting 14 on both sides,
0 = 6 w² - 5 w - 14
Rewriting,
6 w² - 5 w - 14 = 0
Now applying quadratic formula,

Rewriting the formula in terms of w,
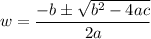
From the 6 w² - 5 w - 14 = 0, value of a = 6 , b = - 5 and c = - 14.
Substituting the values,
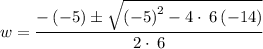
Simplifying,
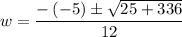
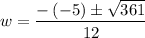
Since √361 = 19,
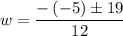
There will be two values of w,
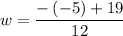 and
and
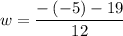
Simplifying,
 and
and
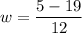
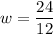 and
and
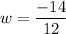
Reducing the fraction in lowest form, divide first expression by 12 and second expression by 2.
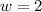 and
and

Since the length of width cannot be negative, so value of w = 2 cm
To find the value of length, Use equation L = 6 w - 5 cm
L = 6 (2) - 5 cm
L = 12 - 5 cm
L = 7 cm
Therefore l = 7 cm and w = 2 cm are the dimensions of the rectangle.