When a base with an exponent is divided by a base with an exponent, you subtract the exponents together. (But you can only combine the exponents when the bases are the same)
For example:
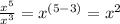
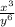 (can't combine the exponents because they have different bases of x and y)
(can't combine the exponents because they have different bases of x and y)
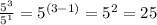
When you multiply an exponent directly to a fraction or a base with an exponent, you multiply the exponents together for each base.
For example:
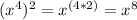
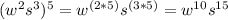 (multiply the exponent to each base, w and s)
(multiply the exponent to each base, w and s)
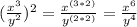 (multiply the exponent to each base/top and bottom of the fraction)
(multiply the exponent to each base/top and bottom of the fraction)
When you have a negative exponent, you move the base with the negative exponent to the other side of the fraction to make the exponent positive.
For example:
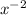 or
or
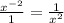
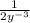 or
or
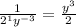
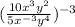 First simplify the fraction inside the parentheses
First simplify the fraction inside the parentheses
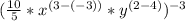
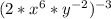 Now multiply the exponents by -3
Now multiply the exponents by -3

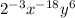 Make all the exponents positive
Make all the exponents positive
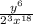 Simplify 2³
Simplify 2³
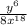 [y^6 ÷ 8x^(18)]
[y^6 ÷ 8x^(18)]