The area of the sector RST is approximately
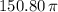 square units. Since the options are given in terms of multiples of
square units. Since the options are given in terms of multiples of
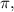 we round to the nearest whole number, which is
we round to the nearest whole number, which is
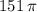 .
.
To find the area of the sector RST of a circle, we can follow these steps:
1. Identify the angle of the sector. In this case, it is 30°.
2. Find the radius of the circle by using the arc length formula, which is
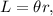 where L is arc length,
where L is arc length,
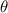 is the angle in radians, and r is the radius.
is the angle in radians, and r is the radius.
3. Calculate the area of the sector, which is
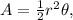 where A is the area, r is the radius, and
where A is the area, r is the radius, and
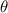 is the angle in radians.
is the angle in radians.
Given that the length of arc ST is
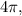 and the angle of the sector is 30°, we first need to convert the angle to radians because the arc length is given in terms of pi, which suggests radians are being used:
and the angle of the sector is 30°, we first need to convert the angle to radians because the arc length is given in terms of pi, which suggests radians are being used:
30° =
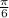 radian
radian
Now, let's use the arc length formula
 to find the radius:
to find the radius:
![\[ 4\pi = (\pi)/(6) r \]](https://img.qammunity.org/2021/formulas/mathematics/middle-school/f7z3ke6ayzhicgqr8m25xvdfh5u4femb2j.png)
Solving for r:
![\[ r = (4\pi)/((\pi)/(6)) \]](https://img.qammunity.org/2021/formulas/mathematics/middle-school/kaj7mr1cg7d3fae4ex1aybxj85f9gc9owa.png)
![\[ r = 4 * 6 \]](https://img.qammunity.org/2021/formulas/mathematics/middle-school/8pjfxmuamfs1teflbxzx4796nmqxpwtckb.png)
![\[ r = 24 \]](https://img.qammunity.org/2021/formulas/mathematics/middle-school/u0q31jtx9wrzshan5pf8uq2ab0xbdiwxim.png)
Now we know the radius of the circle is 24. We can find the area of the sector using the formula
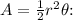
![\[ A = (1)/(2) * (24)^2 * (\pi)/(6) \]](https://img.qammunity.org/2021/formulas/mathematics/middle-school/a4xf1we2579q6qoenk0jvv9h8numwv06cq.png)
A=
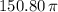 square units
square units