Question

Now that he needs to do schoolwork at home, Oswald decides to see if this trigonometry stuff actually works. He wants to find the height of a tree in his yard. He measures the distance between himself and the tree as 100 feet. His teacher told him about an app on his phone that works like an inclinometer (measures angles up and down; look it up). He uses the app to measure the angle of elevation from his eye level (5.5 feet off the ground) to the top of the tree as 33 degrees. Now he’s stuck, it’s been so long since he’s reviewed trig. Help Oswald and find the height of the tree with the given information.

Answer 1

About 70.44 feet

Explanation:

With the angles that you know, you can form an imagniary triangle with angles 33 degrees, 90 degrees, and 57 degrees. Now, you can use the law of sines to find that
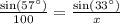`(\sin(57^\circ))/(100)=(\sin(33^\circ))/(x)`. Cross multiplying, you find that x is about 64.94. Adding 5.5 feet to this, you get a total height of 70.44 feet. Hope this helps!