Question

Circle C has diameter AE with a length of 2 cm,

and a central angle with the measure shown.
Find the length of arc DE to the nearest tenth.
Use 3.14 for a
HELP ASAP

Answer 1

We have been given that Circle C has diameter AE with a length of 2 cm, and a central angle with the measure
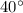`40^(\circ)`. We are asked to find the length of arc DE.

We will use arc length formula to solve our given problem.

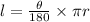`l=(\theta)/(180)* \pi r`, where,

`l` = Arc length,

`\theta` = Central angle in degrees.

r = radius of circle.

Since AE is diameter, so radius will be half of AE.

`r=\frac{2\text{ cm}}{2}=1\text{ cm}`

`l=(40)/(180)* 3.14 * (1\text{ cm})`

`l=(2)/(9)* 3.14 * (1\text{ cm})`

`l=0.697777\text{ cm}`

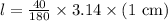
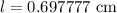
Upon rounding to nearest tenth, we will get:

`l\approx 0.7\text{ cm}`

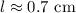
Therefore, the length of arc DE is approximately 0.7 cm.