Answer:
The area of the sector is 33
 .
.
Step-by-step explanation:
A sector is a part of a circle that is formed by two radii (which forms a central angle), and an arc. The area of a sector (in radians) is given by:
= (θ ÷
 ) ×
) ×

where: θ is the central angle of the sector and r is the radius of the circle of which the sector is a part.
Area of a circle =
 . But the area of the circles was given to be 36
. But the area of the circles was given to be 36
 .
.
Area of the sector = (θ ÷
 ) × area of the circle
) × area of the circle
= (θ ÷
 ) ×36
) ×36

θ has been given to be
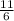
 .
.
Therefore;
Area of the sector = (
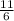
 ÷
÷
 ) ×36
) ×36

=
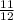 × 36
× 36

= 11 × 3

= 33

The area of the sector is 33
 .
.