Answer:
Approximately
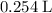 (at STP.)
(at STP.)
Assumption: both
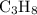 and
and
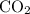 act like ideal gases.
act like ideal gases.
Step-by-step explanation:
Make sure that this chemical equation is properly balanced.
The ratio between the coefficient of
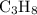 and that of
and that of
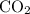 is
is
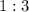 . As a result, for every
. As a result, for every
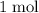 of
of
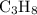 consumed,
consumed,
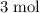 of
of
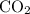 will be produced.
will be produced.
In other words:
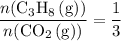 .
.
The coefficients in the balanced equation give a relationship between the number of moles of the two species. One more step is required to obtain a relationship between the volume of these two species.
Under the same pressure and temperature, two ideal gases with the same number of gas particles will have the same volume. Additionally, the volume of an ideal gas is proportional to the number of particles in it.
In this question, if both
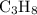 and
and
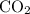 are at STP, their pressure and temperature would indeed be the same. If they are both assumed to be ideal gases, then the ratio between their volumes would be the same as the ratio between the number of moles of their particles. that is:
are at STP, their pressure and temperature would indeed be the same. If they are both assumed to be ideal gases, then the ratio between their volumes would be the same as the ratio between the number of moles of their particles. that is:
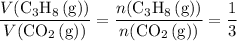 .
.
Therefore, to produce
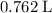 of
of
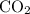 , the minimum volume of
, the minimum volume of
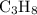 would be:
would be:
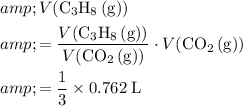 .
.