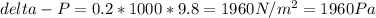Question

A cylindrical block of mass M=50kg and height h=0.2m is hanging on a rope and is in equilibrium. Any difference in atmospheric pressure along the height of the block is negligible.

The cylindrical block is fully immersed in water with density rw=1000 kg/m3 remaining suspended by the rope and in equilibrium. The top of the cylinder is at the surface level. What is the difference of pressure in the bottom to the pressure from the top?

Answer 1

`\Delta P = 1961.4\,Pa`

Step-by-step explanation:

The difference of pressure is given by gauge pressure:

`\Delta P = \rho_(w)\cdot g \cdot \Delta h`

`\Delta P = \left(1000\,(kg)/(m^(3)) \right)\cdot \left(9.807\,(m)/(s^(2)) \right)\cdot (0.2\,m)`

`\Delta P = 1961.4\,Pa`

Answer 2

the difference of pressure in the bottom to the pressure from the top is 1960 Pa

Step-by-step explanation:

Given data:

m = mass of the block = 50 kg

h = height = 0.2 m

ρ = density = 1000 kg/m³

Question: What is the difference of pressure in the bottom to the pressure from the top, ΔP = ?

Let P₁ the pressure on the top and P₂ the pressure in the bottom

`delta-P=P_(1) -P_(2)=h\rho g`

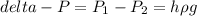
Here, g = gravity = 9.8 m/s²

`delta-P=0.2*1000*9.8=1960N/m^(2) =1960Pa`