Question:
A helicopter flying 1,600 feet above the ground spots an airplane flying above. If the horizontal distance between the helicopter and airplane is 3,055 feet and the angle of elevation is 71°, find the airplane’s altitude.
Answer:
The airplane altitude is 10472.364 ft
Explanation:
The question is related to an angle of elevation problem which we answer as follows;
Altitude of flying helicopter = 1600 ft
Angle of elevation of airplane = 71 °
Horizontal distance between helicopter and airplane = 3055 ft
The vertical distance between the helicopter and the airplane is thus;
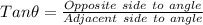
Where the angle is 71 ° as in the question, we have;
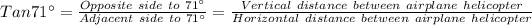
∴ Vertical distance between airplane and helicopter = tan71° × 3055
= 8872.364 ft.
The altitude of the airplane is then;
Altitude of the helicopter + 8872.364 ft
= 1600 + 8872.364 = 10472.364 ft
The airplane altitude = 10472.364 ft.