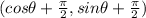Answer:
Considering the point
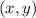
If you represent it as a complext number, you get:
- Counterclockwise if multiplying by

- Clockwise if multiplying by
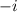
Note, I'm considering
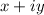
Another approach using trigonometry is considering:
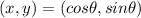
So the rotation will get the coordinates