The area covered by a 3 × 3 array of planters, each with a base of 4 1/5 by 1 1/3 inches, is 50.4 square inches. This is calculated by finding the area of one planter and multiplying it by the total number of planters.
To find the area covered by the planters, you can first find the area of one planter and then multiply it by the total number of planters in the array.
The area of one planter is the product of its length and width:
![\[ \text{Area of one planter} = \left(4 (1)/(5)\right) * \left(1 (1)/(3)\right) \]](https://img.qammunity.org/2021/formulas/mathematics/high-school/5gw9eh17ems6rwly5bu4oyqxia58h0y5sn.png)
To perform this multiplication, convert the mixed numbers to improper fractions:
![\[ \text{Area of one planter} = \left((21)/(5)\right) * \left((4)/(3)\right) \]](https://img.qammunity.org/2021/formulas/mathematics/high-school/anyq3fyfmi4b38f419rmur3l58o97nonkk.png)
Multiply the numerators and denominators:
![\[ \text{Area of one planter} = (21 * 4)/(5 * 3) \]\[ \text{Area of one planter} = (84)/(15) \]](https://img.qammunity.org/2021/formulas/mathematics/high-school/3zmnab7lzumutvb9uvk3e99w1rxr95fmfb.png)
Now, simplify the fraction:
![\[ \text{Area of one planter} = (28)/(5) \]](https://img.qammunity.org/2021/formulas/mathematics/high-school/hy3cbqannq2lofxepwa891fdc38pfdri1x.png)
So, the area of one planter is
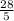square inches.
Since there is a 3 × 3 array of these planters, multiply the area of one planter by the total number of planters:
![\[ \text{Total area} = (28)/(5) * 3 * 3 \]\[ \text{Total area} = (28 * 9)/(5) \]](https://img.qammunity.org/2021/formulas/mathematics/high-school/axt1r978uqjj9hqxa3i7xj0hstba4bu870.png)
Total area =
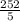
Simplify the fraction:
Total area = 50.4
Therefore, the area covered by the planters is 50.4 square inches.
The complete question is:
In a greenhouse, basil is grown in planters that have a base of 4 1/5 in by 1 1/3 in. If there is a 3 × 3 array of these planters with no space between them, what is the area covered by the planters?