Question

Craign has a building block in the shape of a rectangular pyramid .A net of which is shown below.If a measures 12 cm b measures 6 cm and d measures 13 cm what is the surface area of the rectangular pyramid

Answer 1

Option D) 294 sq cm is correct

∴ the surface area of the rectangular pyramid is 294 sq cm

Explanation:

First we have to split the net into 4 triangles and 1 rectangle

Given a = 12 cm ,b = 6 cm and d = 13 cm

To find the surface area of the rectangular pyramid:

Now find the area of the rectangle base

`Rectangle base area=b* a`

`= 6* 12`

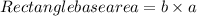
= 72 sq. cm

∴ Rectangle base area=72 sq cm

Now to find the area of the triangle on the left

`Left triangle=(1)/(2)(b)(d)`

`=(1)/(2)(6)(13)`

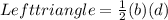
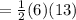
= 39 sq cm

∴ Left triangle=39 sq cm

Since all the triangles are congruent , you will need to multiply by 2 to get the combined area of the triangle on the left and on the right.

Area of left and right triangles= 2(39)

=78 sq cm

∴ Area of left and right triangles=78 sq cm

Find the area of the triangle on the bottom

`Bottom triangle area=(1)/(2)(a)(a)`

`=(1)/(2)(12)(12)`

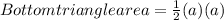
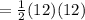
= 72 sq cm

∴ Bottom triangle area=72 sq cm

Since the bottom of the triangle is congruent to the top triangle, multiply that by 2 to get a combined area of the triangle on the bottom and top

Area of top & bottom triangles=2 (72)

= 144 sq cm

∴ Area of top & bottom triangles= 144 sq cm

Finally add the area of the 4 triangles to the area of the rectangular base we get

=72 + 78 + 144

= 294 sq cm

∴ the surface area of the rectangular pyramid is 294 sq cm

∴ option D) 294 sq cm is correct.